17 The Area-Based Approach (ABA) to forest modelling
This section presents a complete workflow about processing ALS point cloud data to create wall-to-wall predictions of selected forest stand attributes using an area-based approach (ABA) to forest inventories. The steps used in this vignette as well as further details about enhanced forest inventories (EFI) are described in depth in White et al. 2013 and White et al. 2017. This vignette assumes that the user has a directory of classified and normalized .las/.laz files. First we load the package sf to work with spatial data.
library(sf)17.1 Read in data
The function readLAScatalog() seen in Chapter 15 builds a LAScatalog object from a folder. Make sure the ALS files have associated index files - for details see: Speed-up the computations on a LAScatalog.
ctg <- readLAScatalog("folder/")
print(ctg)
#> class : LAScatalog
#> extent : 297317.5 , 316001 , 5089000 , 5099000 (xmin, xmax, ymin, ymax)
#> coord. ref. : +proj=utm +zone=18 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs
#> area : 125.19 km²
#> points : 1.58 billion points
#> density : 12.6 points/m²
#> num. files : 138
plot(ctg)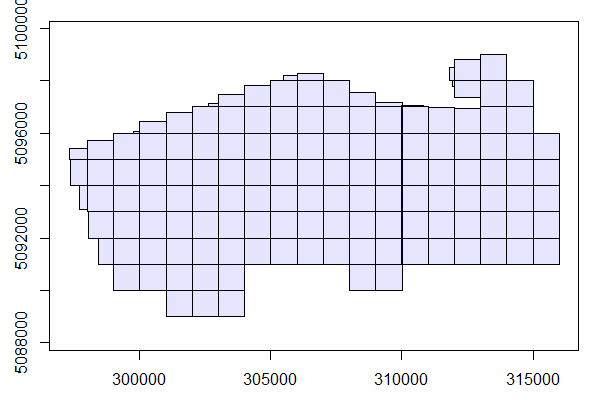
Now that our ALS data is prepared lets read in our inventory data using the st_read() function from the sf package. We read in a .shp file where each features is a point with a unique plot ID and corresponding plot level inventory summaries.
plots <- st_read("PRF_plots.shp")Our plots object contains 203 plots with coordinates of plot centers, plot name, and stand attributes: Lorey’s height (HL), Basal area (BA), and gross timber volume (GTV).
plots
#> Simple feature collection with 203 features and 4 fields
#> geometry type: POINT
#> dimension: XY
#> bbox: xmin: 299051.3 ymin: 5089952 xmax: 314849.4 ymax: 5098426
#> epsg (SRID): NA
#> proj4string: +proj=utm +zone=18 +ellps=GRS80 +units=m +no_defs
#> First 5 features:
#> PlotID HL BA GTV geometry
#> 1 PRF002 20.71166 38.21648 322.1351 POINT (313983.8 5094190)
#> 2 PRF003 19.46735 28.92692 251.1327 POINT (312218.6 5091995)
#> 3 PRF004 21.74877 45.16215 467.1033 POINT (311125.1 5092501)
#> 4 PRF005 27.76175 61.55561 783.9303 POINT (313425.2 5091836)
#> 5 PRF006 27.26387 39.78153 508.0337 POINT (313106.2 5091393)To visualize where the plots are in our study area we can overlay them on the LAScatalog.
plot(ctg)
plot(plots, add = TRUE, col = "red")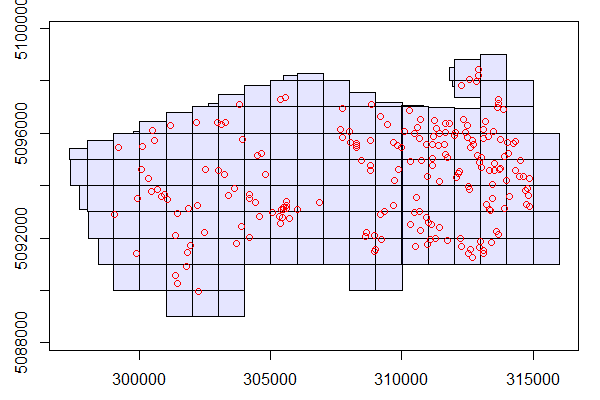
We have now prepared both our ALS and plot inventory data and can begin ABA processing.
17.2 ABA database building
To build a database ready for modeling the steps are the following:
- Clip the regions of interest (stands) using a shapefile of stand locations.
- Calculate derived metrics for each stand.
- Associate stand attributes (ID,HL,BA,GTV) to the metrics.
This can be done with a single function plot_metrics(). We also use the opt_filter() function on the LAScatalog to ignore noise below 0 m at read time so that they do not influence future processing. We clip discs with a radius of 14.1 meters because our plot radius is 14.1 m.
opt_filter(ctg) <- "-drop_z_below 0" # Ignore points with elevations below 0
D <- plot_metrics(ctg, .stdmetrics_z, plots, radius = 14.1)We have now calculated a variety of ALS metrics for each plot.
17.3 Statistical modeling
Here we provide a simple example of how to create an OLS model (lm) for Lorey’s Mean Height (HL). Using the summary and plot functions we found that the 85th percentile of height (zq85) for ALS metrics explain a large amount of variation in HL values. We are more than happy with this simple model.
m <- lm(HL ~ zq85, data = D)
summary(m)
#> Call:
#> lm(formula = HL ~ zq85, data = D)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.640 -1.053 -0.031 1.030 4.258
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 2.29496 0.31116 7.376 4.2e-12 ***
#> zq85 0.93389 0.01525 61.237 < 2e-16 ***
#> ---
#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#>
#> Residual standard error: 1.5 on 201 degrees of freedom
#> Multiple R-squared: 0.9491, Adjusted R-squared: 0.9489
#> F-statistic: 3750 on 1 and 201 DF, p-value: < 2.2e-16Here we visualize the relationship between the observed (measured) and predicted (ALS-based) HL values.
plot(D$HL, predict(m))
abline(0,1)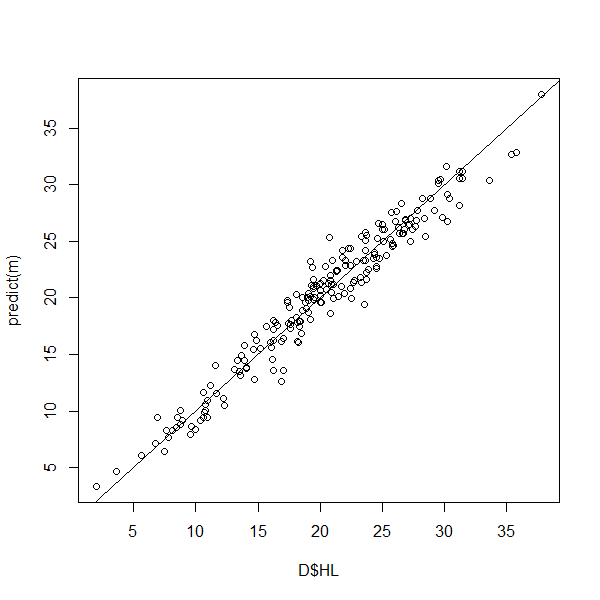
17.4 Wall to wall modelling
Now that we have created a model using plot data, we need to apply that model across our entire study area.
To do so we first need to generate the same suite of ALS metrics (.stdmetrics_z) for our ALS data using the pixel_metrics() function on our original collection of files. Note that the res parameter is set to 25 because we want the resolution of our metrics to match the area of our sample plots (14.1 m radius = 625m2).
metrics_w2w <- pixel_metrics(ctg, .stdmetrics_z, res = 25, pkg = "terra")To visualize any of the metrics you can use the plot function.
plot(metrics_w2w$zq85)
plot(metrics_w2w$zmean)
plot(metrics_w2w$pzabovezmean)17.5 Calculate wall-to-wall predictions
We can use the predict() function to produce HL_pred which is a wall-to-wall raster of predicted Lorey’s mean height.
HL_pred <- predict(metrics_w2w, m)To visualize wall-to-wall predictions use
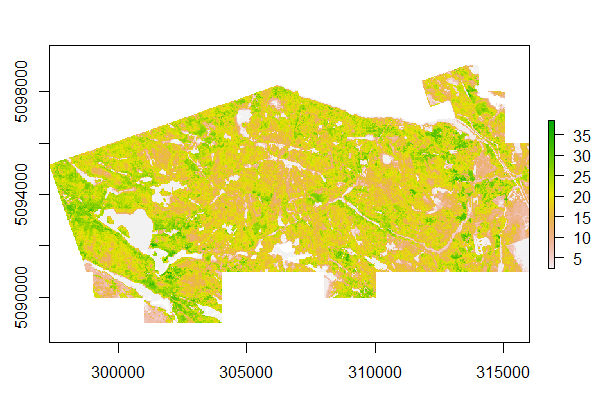
plot(HL_pred)